Číselné soustavy a převody mezi nimi
Číselná soustava je způsob reprezentace čísel.Máme v zásadě 2 druhy číselných soustav:
- poziční (dekadická, binární, oktálová, hexadecimální)
- nepoziční (římská, grayův kód)
Poziční soustavy
Libovolně velké číslo určené pomocí poziční soustavy lze zapsat pomocí konečně mnoho předem zvolených symbolů jež
nabývají různé hodnoty podle toho, na kterém místě se vyskytují (pozice čísla udává mocnina základu).
Nebo jinak řečeno: každá číslice v zápisu čísla má hodnotu, která je určena její pozicí v tomto čísle - řádem.
Libovolné číslo R lze zapsat mnohočlenem:

kde Z je základ, m - počet řádových míst, ai - jednotlivé koeficienty na jednotlivých řádových místech čísla, n - počet desetinných míst. Tento zápis se občas nazývá Hornerovo schéma.
Desítková soustava (dekadická)
- poziční číselná soustava běžně užívaná v každodenním životě.
- Má základ Z=10 nejspíše už pro to, jelikož člověk má 10 prstů.
- Soustava používá číslice 0 až 9. Není však vhodná pro číslicové systémy, jelikož by se muselo rozlišovat 10 různých stavů, například napěťových úrovní. To by bylo velice obtížné a proto se používá dvojková (binární) soustava, která má pouze dva stavy (0,1).
- častokrát označována písmenem D
Dvojková soustava (binární)
- číselná soustava o základu Z = 2
- soustava využívá pouze dvě číslice (0 a 1), z čehož plynou nesporné výhody pro využití v číslicové technice.
- označována písmenem B
Osmičková soustava (oktálová)
- číselná soustava o základu Z = 8
- využívá osmi číslic (0,1,2,3,4,5,6,7)
- každý symbol oktalové soustavy odpovídá 3 bitům dvojkové soustavy
- označováno častokrát písmenem O
Šestnáctková soustava (hexadecimální)
- číselná soustava o základu Z = 16
- jelikož nemáme 16 různých číslic, používá se při zápisu šestnáctkové soustavy číslice 0 až 9 a písmena A až F (A = 10, B = 11, C = 12, D = 13, E = 14, F = 15)
- používá se v mikropočítačové technice například k popisu dat na adresové a datové sběrnici
- každý symbol hexadecimální soustavy odpovídá 4 bitům dvojkové soustavy.
- při zápisu se často označuje písmenem H (případně h), například číslo 8Eh se dá vyjádřit v dvojkové soustavě jako 1000 1110.
| Desítková | Dvojková | Osmičková | Šestnáctková |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Převody mezi číselnými soustavami
Převod čísla z dekadické soustavy do jakékoliv jiné
a) metoda postupného dělení
Číslo v desítkové soustavě postupně dělíme 2 (případně jiným základem) až je podíl roven 0. Zárověň zapisujeme zbytky po dělení. Čteme-li je v obráceném pořadí, získáme výsledek.

b) metoda odečítání mocnin základu
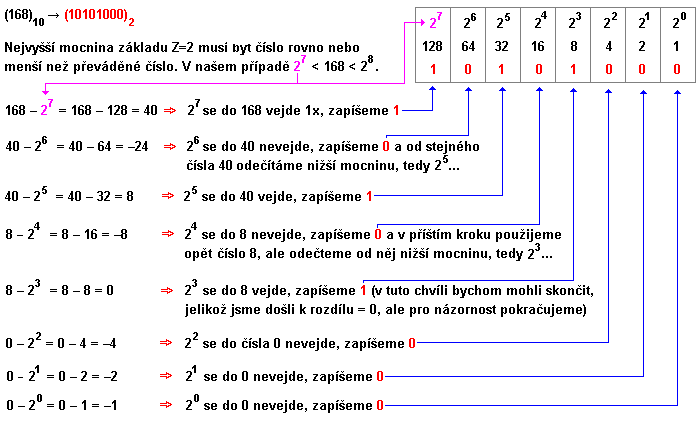
Tuto metodu si ukážeme na příkladu převodu čísla (168)10 do binární soustavy. Postupujeme tak, že si nejprve vyjádříme mocniny základu soustavy, do níž chceme dekadické číslo převést, přičemž nejvyšší vyjádřená mocnina základu Z bude číslo rovno nebo menší než převáděné číslo. V našem případě nejvyšší mocninou bude 27, jelikož 27 < 168 < 28. Další postup by měl být zřejmý ze schématu.
Převody mezi oktalovou, hexadecimální a binární soustavou
Pokud je základ jedné soustavy mocninou základu soustavy druhé, lze čísla převádět zjednodušeným postupem.
Pro převod z binární soustavy do oktalové, binární číslo rozdělíme na trojice. (lze si pamatovat jako 23 = 8). Pokud chceme převést číslo z oktalové do binární, postupujeme opačně, tedy jednotlivé cifry vyjádříme v binární podobě a získáme číslo v dvojkové soustavě.

Při převádění čísla z hexadecimální soustavy do binární, se binární číslo rozdělí na čtveřice. (lze si pamatovat jako 24 = 16)
